Cách tính hệ số góc của đường thẳng là một khái niệm quan trọng để xác định độ dốc và hướng của các tuyến đường, công trình hoặc các đối tượng địa hình trên mặt phẳng tọa độ. Việc hiểu và tính toán chính xác hệ số góc giúp kỹ sư trắc địa đảm bảo tính chính xác của các bản đồ, kế hoạch thiết kế và thi công công trình.Công cụ hỗ trợ công tác đo đạc hệ số góc là máy thủy bình. Hãy cùng Việt Thanh group tìm hiểu về cách tính hệ số góc của đường thẳng.
Cách tính hệ số góc của đường thẳng
Hệ số góc của đường thẳng (được ký hiệu là m) là một giá trị số đo độ dốc của đường thẳng so với trục hoành (trục x) trên mặt phẳng tọa độ. Nó cho biết sự thay đổi của trục tung (trục y) khi trục hoành thay đổi một đơn vị. Hệ số góc là một phần không thể thiếu trong việc mô tả đặc tính của một đường thẳng và nó cung cấp nhiều thông tin về cách mà đường thẳng đó thay đổi trên mặt phẳng.
Công tính hệ số góc
Hệ số góc của đường thẳng được xác định bằng công thức:
m=(y2−y1)/(x2−x1)m = (y2 - y1) / (x2 - x1)m=(y2−y1)/(x2−x1)
Trong đó:
- y2 - y1 là sự thay đổi của giá trị y (độ cao) giữa hai điểm trên đường thẳng.
- x2 - x1 là sự thay đổi của giá trị x (độ dài ngang) giữa hai điểm đó.
Ví dụ:
Để tính hệ số góc của đường thẳng đi qua hai điểm A(x1, y1) và B(x2, y2), ta áp dụng công thức:
m=(y2−y1)/(x2−x1)m = (y2 - y1) / (x2 - x1)m=(y2−y1)/(x2−x1)
Ví dụ: Cho hai điểm A(1, 2) và B(3, 6). Tính hệ số góc của đường thẳng đi qua hai điểm này.
Áp dụng công thức:
m=(6−2)/(3−1)=4/2=2m = (6 - 2) / (3 - 1) = 4 / 2 = 2m=(6−2)/(3−1)=4/2=2
Vậy, hệ số góc của đường thẳng đi qua hai điểm A và B là 2.
Một số thương hiệu điển hình trong công tác tính hệ số góc của máy thủy bình như máy thủy bình Hi-Target, máy thủy bình Satlab….Ngoài ra, Việt Thanh Group có dịch vụ cho thuê thiết bị đo đạc uy tín, chất lượng.
>>>Xem thêm: Cách tính giá đền bù đất quy quy hoạch hiện nay
Hệ số góc và phương trình đường thẳng
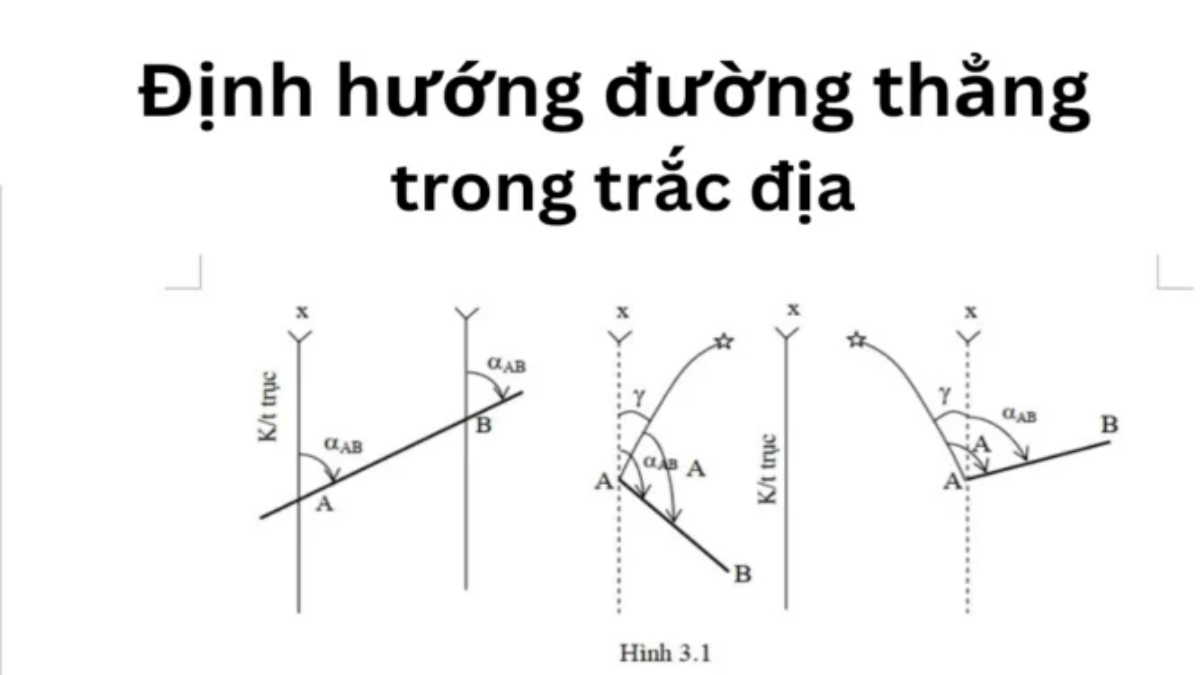
Phương trình tổng quát của đường thẳng trong mặt phẳng tọa độ có dạng:
y=mx+by = mx + by=mx+b
Trong đó:
- m là hệ số góc của đường thẳng.
- b là hằng số, đại diện cho giao điểm của đường thẳng với trục tung (trục y).
Nếu bạn biết hệ số góc m và một điểm (x1, y1) nằm trên đường thẳng, bạn có thể tìm được b bằng cách giải phương trình:
y1=mx1+by1 = mx1 + by1=mx1+b b=y1−mx1b = y1 - mx1b=y1−mx1
Ví dụ: Cho điểm C(2, 3) và hệ số góc m = 2. Tìm phương trình của đường thẳng đi qua điểm này.
Từ công thức trên:
b=3−2×2=3−4=−1b = 3 - 2 \times 2 = 3 - 4 = -1b=3−2×2=3−4=−1
Vậy, phương trình của đường thẳng là:
y=2x−1y = 2x - 1y=2x−1
Ý nghĩa của hệ số góc của đường thẳng
Hệ số góc của đường thẳng cho biết đường thẳng đó dốc lên hay dốc xuống và mức độ dốc của nó. Cụ thể:
- Hệ số góc dương: Đường thẳng dốc lên khi di chuyển từ trái sang phải.
- Hệ số góc âm: Đường thẳng dốc xuống khi di chuyển từ trái sang phải.
- Hệ số góc bằng 0: Đường thẳng song song với trục hoành (trục x).
- Hệ số góc không xác định (vô cực): Đường thẳng song song với trục tung (trục y).
Các trường hợp đặc biệt
- Đường thẳng song song với trục tung: Khi đường thẳng song song với trục tung, hệ số góc không xác định vì x2 - x1 = 0.
- Đường thẳng song song với trục hoành: Khi đường thẳng song song với trục hoành, hệ số góc bằng 0 vì y2 - y1 = 0.
>>>Xem thêm: Cách tính chi phí san lấp mặt bằng chuẩn xác
Tầm quan trọng của hệ số góc của đường thẳng
Việc hiểu và tính chính xác hệ số góc của đường thẳng có ý nghĩa quan trọng trong nhiều lĩnh vực như toán học, vật lý, kỹ thuật và kinh tế. Nó giúp xác định hướng, độ dốc và mối quan hệ giữa các điểm trong không gian hai chiều.
Trong thực tế, hệ số góc của đường thẳng được sử dụng trong nhiều lĩnh vực khác nhau. Ví dụ:
- Trong kỹ thuật xây dựng: Hệ số góc được sử dụng để xác định độ dốc của mái nhà, đường giao thông, và các cấu trúc khác.
- Trong kinh tế: Hệ số góc được sử dụng để phân tích xu hướng của dữ liệu, ví dụ như xu hướng tăng trưởng doanh số bán hàng theo thời gian.
- Trong vật lý: Hệ số góc được sử dụng để mô tả chuyển động của các vật thể trong không gian hai chiều.
>>>Xem thêm: Cách tính mực nước biển chi tiết nhất
Hệ số góc của đường thẳng là một công cụ quan trọng để hiểu rõ hơn về độ dốc và hướng của đường thẳng trong mặt phẳng tọa độ. Bằng cách nắm vững cách tính hệ số góc, bạn có thể giải quyết nhiều bài toán liên quan đến hình học phân tích một cách dễ dàng và chính xác.Để tìm hiểu thêm về các khái niệm liên quan và nhận được sự tư vấn chuyên sâu, vui lòng truy cập Việt Thanh Group. Tại đây, bạn sẽ được hỗ trợ và cung cấp thông tin chi tiết về các phương pháp tính toán và ứng dụng của hệ số góc trong thực tiễn.

.jpg)