Tập hợp số là gì? Các tập hợp số trong toán học là kiến thức vô cùng quan trọng. Sau đây hãy cùng Bamboo tìm hiểu kiến thức về tập hợp số trong toán học này nhé!!
Tập hợp số là gì? Ví dụ về tập hợp số
Tập hợp số là một nhóm các số nhất định. Các số này được gọi là phần tử của tập hợp.

Một vài ví dụ về tập hợp số:
- Tập hợp các số trên mặt đồng hồ => các phần tử là: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12.
- Tập hợp các số tự nhiên = > N={0; 1; 2; 3;…}
- Tập hợp các số tự nhiên các số từ 0 cho đến 99
Các loại tập hợp số cơ bản
Tập hợp các số tự nhiên quy ước là N
N={0, 1, 2, 3, 4, 5, ..}.
Tập hợp các số nguyên quy ước là Z
Z={…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}.
Tập hợp số nguyên bao gồm các phân tử là các số tự nhiên và các phần tử đối của các số tự nhiên.
Tập hợp của các số nguyên dương kí hiệu là N*
Tập hợp các số hữu tỉ quy ước là Q
Q={ a/b; a, b∈Z, b≠0}
Một số hữu tỉ có thể được biểu diễn bằng một số thập phân hữu hạn hoặc số thập phân vô hạn tuần hoàn.
Tập hợp các số thực quy ước là R
Mỗi số được biểu diễn bằng một số thập phân vô hạn không tuần hoàn được ta gọi là một số vô tỉ. Tập hợp các số vô tỉ được quy ước kí hiệu là I. Tập hợp của các số thực bao gồm các số hữu tỉ và các số vô tỉ.
Mối quan hệ của tập hợp số
N: tập hợp các số tự nhiên
Z: tập hợp các số nguyên
Q: tập hợp các số hữu tỉ
R: tập hợp số thực
Mối quan hệ của chúng là: N ⊂ Z ⊂ Q ⊂ R
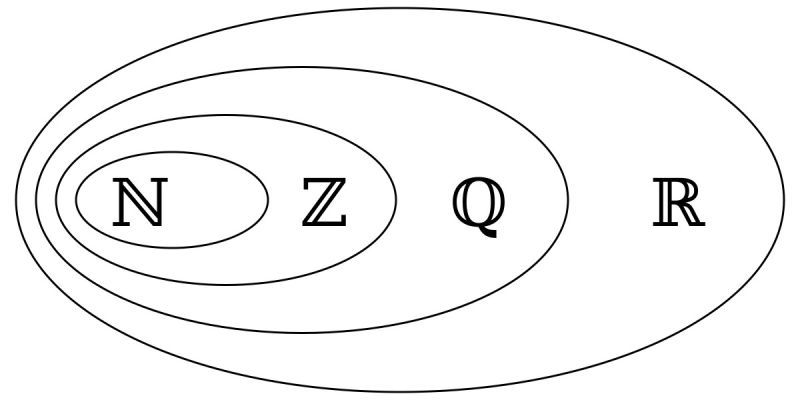
Mối quan hệ giữa các tập hợp thể hiện trực quan qua biểu đồ Ven
Một số tập hợp con của tập hợp số thực
Ví dụ a, b là 2 số thực (a
Khi đó [a;b)={x∈R|a≤x
Với A và B là các tập con kể trên của tập số thực. Ta có:
Cách xác định giao của A và B
Bước 1. Biểu diễn A, Biểu diễn B trên cùng 1 trục số.
Bước 2. Lấy phần không bị gạch chéo.
Bước 3. Kiểm tra các điểm đặc biệt để tránh nhầm lẫn.
Cách xác định hợp của A và B
Bước 1. Biểu diễn A, Biểu diễn B trên cùng 1 trục số. Lưu ý không gạch chéo mà tô đậm miền của A và miền của B.
Bước 2. Lấy phần tô đậm.
Bước 3. Kiểm tra các điểm đặc biệt để tránh nhầm lẫn.
Cách xác định hiệu của A cho B
Bước 1. Biểu diễn A, Biểu diễn B trên cùng 1 trục số.
Bước 2. Gạch chéo miền của B.
Bước 3. Lấy phần không bị gạch chéo.
Bước 4. Kiểm tra các điểm đặc biệt để tránh nhầm lẫn.
Các phép toán trong tập hợp của toán học
Các phép toán trên tập hợp bao gồm phép hợp, phép giao, phép hiệu và phép lấy phần bù.
- Phép hợp: A∪B⇔{x∣x∈A hoặc x∈B}
Tập hợp các phần tử thuộc A hoặc thuộc B., ký hiệu: A∪B
- Phép giao: A∩B⇔{x∣x∈A và x∈B}
Tập hợp các phần tử giao cả A và B., ký hiệu:A∩B
- Phép hiệu: A∖B=x∣x∈A & x∉B
Tập hợp các phần tử thuộc A nhưng không thuộc B, ký hiệu: A∖B
- Phép lấy phần bù:
Cho A là tập con của tập E. Phần bù của A trong X là X∖A, ký hiệu : CXA là tập hợp cả các phần tử của E mà không là phần tử của A.
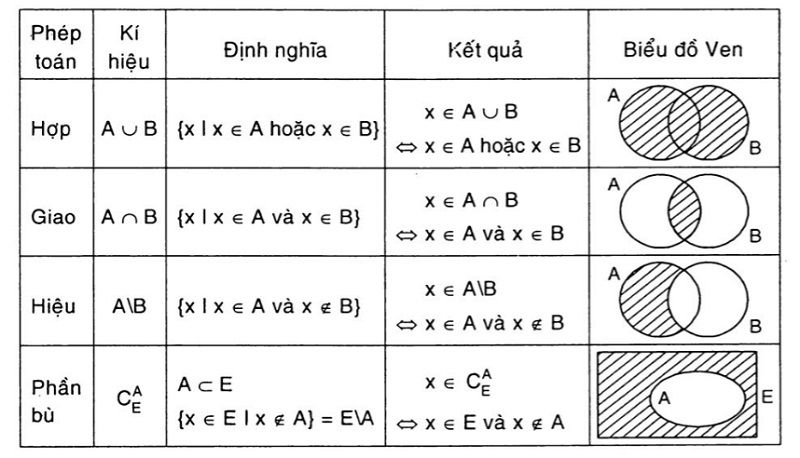
Các phép toán trong tập hợp của toán học
Bài tập tham khảo về tập hợp số
Câu 1: Cho tập hợp A = {x ∈ R | -3
A. {-3; 1}.
B. [-3; 1].
C. [-3; 1).
D. (-3; 1).
Hướng dẫn:
=>Chọn D.
Theo lý thuyết: (a;b) = {x ∈ R | a
Vậy A = {x ∈ R | -3
Câu 2: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?
A.
B.
C.
D.
Hướng dẫn:
=>Chọn A. Vì (1; 4] gồm các số thực x mà 1
Đáp án B sai vì [1; 4] gồm các số thực x mà 1 ≤ x ≤ 4 .
Đáp án C sai vì (1; 4) gồm các số thực x mà 1
Đáp án B sai vì [1; 4) gồm các số thực x mà 1 ≤ x ≤ 4.
Câu 3: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A = { x ∈ R | 4 ≤ x ≤ 9} :
A. A = [4; 9].
B. A = (4; 9].
C. A = [4; 9).
D. A = (4; 9)
Hướng dẫn:
=> Chọn A.
Theo lý thuyết: [a;b] = {x ∈ R | a ≤ x ≤ b} . Suy ra A = {x ∈ R | 4 ≤ x ≤ 9} = [4; 9].
Câu 4: Cho hai tập hợp A = [-2; 7); B = (1; 9]. Tìm A ∪ B.
A. (1; 7).
B. [-2; 9].
C. [-2; 1).
D. (7; 9].
Hướng dẫn:
=> Chọn B.
Ta biểu diễn tập hợp A và B trên trục số như sau:
Vậy A ∪ B = [-2;7] ∪ (1;9] = [-2;9] .
Xem thêm:
- R trong toán học là gì? Định nghĩa, tính chất và bài tập minh họa có giải
- Cách tính trung bình cộng và các bài toán trung bình cộng cơ bản và nâng cao
- Số hữu tỉ là gì? Số vô tỉ là gì? Phân biệt số hữu tỉ và vô tỉ
Như vậy, với những thông tin bổ ích trên. Các bạn đã hiểu hơn về khái niệm cũng như các chuyên đề xoay quanh tập hợp số là gì? Chúc mọi người học tập thật tốt và áp dụng kiến thức chính xác trong quá trình học tập của mình.