Momen quán tính là gì? Những yếu tố nào thúc đẩy tới momen quán tính? Công thức tính momen quán tính ra sao? Đó là thắc mắc của nhiều độc giả đã gửi về cho LabVIETCHEM trong thời kì qua và trong bài viết ngày hôm nay, chúng tôi sẽ giúp người mua trả lời những thắc mắc đó.
Nội Dung Bài Viết
Giảng giải khái niệm momen quán tính là gì?
Momen quán tính là đại lượng vật lý đặc trưng cho mức quán tính của những vật thể ở trong đi lại quay, giống như khối lượng trong đi lại thẳng. Hiểu một cách đơn thuần thì momen quán tính là đại diện cho lực cản của vật thể thay đổi véc tơ vận tốc tức thời góc, theo cách giống như cách khối lượng biểu thị khả năng chống lại sự thay đổi véc tơ vận tốc tức thời trong đi lại ko quay (đi lại thẳng), theo định luật đi lại của Newton.
Nó được xác định dựa trên sự phân bố khối lượng trong vật thể và vị trí của trục nên dù là cùng một đối tượng thì những giá trị quán tính vấn với thể rất khác nhau, tùy thuộc vào vị trí và hướng của trục quay.

Momen quán tính là gì
Những công thức tính momen quán tính
1. Công thức chung
Căn cứ vào khái niệm của momen quán tính, chúng ta với công thức tính như sau:
I = m.r2
Trong đó:
- M là khối lượng của vật mẫu
- r là khoảng cách từ vật tới trục quay
Với hệ nhiều khối lượng với kích thước nhỏ thì momen quán tính của hệ được tính bằng tổng của momen quán tính từng khối lượng:
2. Công thức tính bằng tích phân
Công thức chung chỉ ưa thích cho những vật thể được coi là tập hợp điểm riêng biệt và với thể được thêm vào tương đối dễ dàng. Nó sắp như ko thể ứng dụng cho những đối tượng phức tạp hơn. Lúc này, bạn cần tiêu dùng công thức tính tích phân cho toàn bộ khối lượng. Giá trị độ to momen lực chính là hàm mật độ khối tại mỗi điểm r.
I = ∑i.mi.ri2
3. Hình cầu rỗng
Muốn xác định độ to momen quán tính cho những vật thể quay quanh trục đi qua tâm quả cầu với hình dạng cầu rỗng với thành mỏng ko đáng kể, ta sử dụng công thức như sau:
I = (2/5).m.r2
Trong đó, m là khối lượng vật rắn và r là bán kính của quả cầu
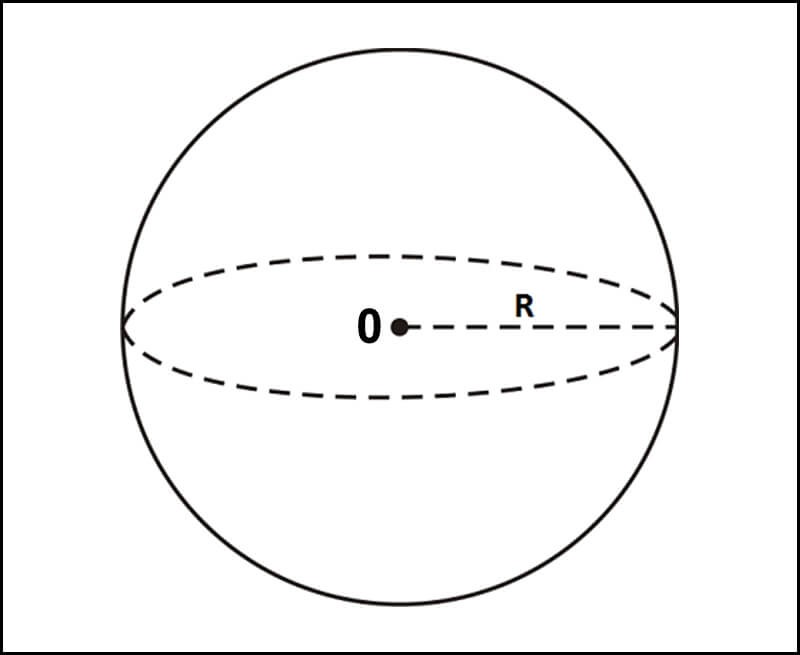
Tính momen quán tính của hình cầu rỗng
4. Quả cầu rắn
Đối với những vật quay hình cầu rắn với thành dày, công thức xác định momen quán tính sẽ là:
I = (2/3).m.r2
Trong đó, m là khối lượng vật rắn và r là bán kính của quả cầu
5. Vật thể với hình dạng chữ nhật với trục quay xuyên tâm
Với những vật quay hình dạng chữ nhật mỏng, thực hiện thao tác quay ở trên trục vuông góc với tâm của tấm (trục quay xuyên tâm) thì độ to của momen quán tính được xác định theo công thức sau:
I = (1/12).m.(a2 + b2 )
Trong đó: m là khối lượng của vật, a là chiều dài hình chữ nhật và b là chiều rộng của vật thể hình chữ nhật.

Vật thể với hình dạng chữ nhật với trục quay xuyên tâm
6. Xi lanh rắn
Một hình trụ đặc với khối lương M quay trên một trục đi xuyên qua tâm của hình trụ với bán kính R với momen quán tính được xác định theo công thức:
I = (1/2).M.R2
7. Xi lanh rỗng với thành mỏng
Đối với một hình trụ rỗng với khối lượng M, thành mỏng, với thể coi là độ dày thành ko đáng kể quay trên một trục đi qua tâm của hình trụ với bán kính R sẽ với momen quán tính được xác định như sau:
I = M.R
Xi lanh rỗng với thành mỏng
8. Hình trụ rỗng
Công thức momen quán tính của hình trụ rỗng khối lượng M với trục quay trên một trục đi qua tâm của hình trụ với bán kính trong là R1 và bán kính ngoài là R2 được xác định là:
I = (1/2). M.( R12 + R22)

Hình trụ rỗng
9. Thanh mảnh với trục xuyên qua một đầu
Một thanh mảnh với khối lượng M lúc quay trên một trục đi qua đầu que vuông góc với chiều dài L của nó sẽ với momen quán tính được xác định như sau
I = (1/3).M.L2
Công thức dời trục hay định lý Huyghen
Momen quán tính với trục ban sơ sẽ được xác định bằng tổng của momen quán tính với trục đi qua tâm music music với tích khối lượng vật và bình phương khoảng cách giữa hai trục, cụ thể như sau:
I0 = I1+m.d2.I0 = I1 + m.d2
Trong đó:
- I0 là momen quán tính đối với trục ban sơ
- I1 là momen quán tính đối với trục mới
- m là khối lượng của vật
- d là khoảng cách giữa hai trục
Một số công thức liên quan khác
Công thức tính toán hai đại lượng chính trong đi lại quay với điều kiện là momen quán tính của một vật đi lại quay quanh một vật nhất quyết.
Động năng quay: Ok = l.ω2.Ok = l.ω2
Động lượng góc: L = l.ω.L = l.ω
Trong đó, L là momen động lượng, l là momen quán tính và ω là véc tơ vận tốc tức thời góc quay.
Một số bài tập minh họa của momen quán tính
Bài tập 1: Cho hai đĩa tròn với momen quán tính là I1 = 5.10-2 kg.m2 và I2 = 3.10-2 kg.m2 quay đồng trục và cùng chiều với tốc độ góc tuần tự tương ứng là ω1 = 10 rad/s và ω2= 20 rad/s. Sau đó hai đĩa tròn này dính lại với nhau và cùng quay với tốc độ góc ω. Tính véc tơ vận tốc tức thời góc ω lúc đã bỏ qua ma sát ở trục quay.
Hướng dẫn giải:
Ứng dụng định luật bảo toàn momen động lượng: I1 . ω1 + I2 . ω2 = (I1 + I2) . ω
⇒ ω = (I1 . ω1 + I2 . ω2 )/ (I1 + I2) = (5.10−2.10 + 3.10−2.20)/(5.10−2 + 3.10−2) = 13,75 (rad/s)
Bài tập 2: Trong đi lại quay của một vật rắn, đại lượng như khối lượng trong đi lại của chất điểm được gọi là:
A - Momen động lượng.
B - Momen quán tính.
C - Momen lực.
D - Tốc độ góc
Hướng dẫn giải
Momen quán tính là đại lượng đặc trưng cho mức quán tính trong đi lại quay của vật rắn và khối lượng đặc trưng cho mức quán tính của chất điểm nên đáp án sẽ là B - Momen quán tính.
Trên đây là một số vấn đề liên quan tới momen quán tính mà LabVIETCHEM muốn san sớt tới độc giả. Hy vọng rằng, đây sẽ là những thông tin hữu ích mà bạn với thể ứng dụng trong học tập và thực hiện.
Website: https://copphaviet.com